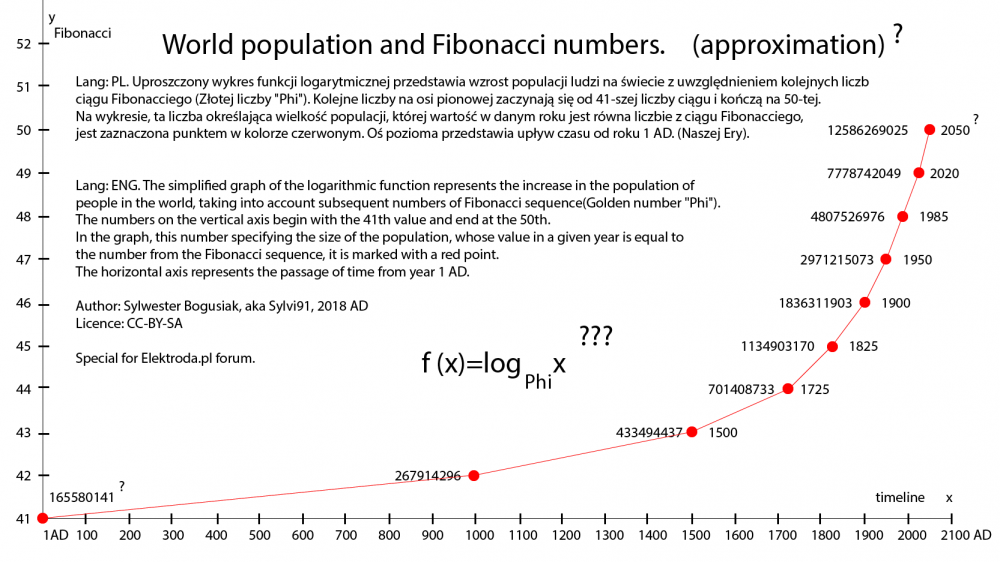
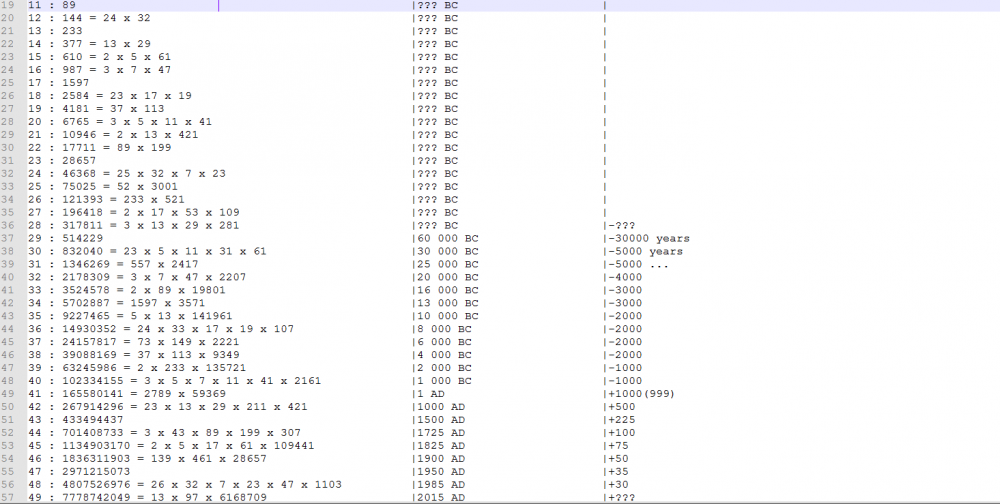
Liczby pierwsze na spirali Fibonacciego.
Kolejny mój wpis w związku z zabawą liczbami.
Tym razem postanowiłem połączyć dwa ciekawe zbiory.
Nie widziałem podobnego rysynku w sieci więc uznałem, że przeprowadzę eksperyment i sam wyrysuję programowo spiralę, a następnie naniosę liczby Fibonacciego oraz liczby Pierwsze.
Gdyby była już taka spirala komuś znana to całkiem dobrze się składa, bo to co ja zauważam może jest wiadome, ale nie było dla mnie jeszcze przed eksperymentem.
Otóż liczby pierwsze na spirali występują w bardzo losowy sposób, to jest pewne.
Przybywa ich pomiedzy kolejnymi wyrazami ciągu Fibonacciego, to jest pewne.
Z obserwacji wynika też coś takiego, że:
Suma liczb pierwszych na spirali pomiędzy kolejnymi wyrazami ciągu Fibonacciego podzielona przez ilość liczb pierwszych, a następnie podzielona przez większą liczbę Fibonacciego daje w przybliżeniu połowę Złotej liczby Phi.
Innymi słowy: suma liczb pierwszych wskazana na spirali w polu każdego kwadratu podzielona przez (ilość liczb pierwszych pomnożoną przez wyższą liczbę Fibonacciego zawsze w wyniku daje nam przybliżenie połowy Złotej liczby.
Wyjątkiem jest początek spirali, gdzie wartości są równe 1.
Czyli zbiór jest w pewnym sensie związany ze złotą spiralą w ten sposób. Czy może to zbyt naciągany wniosek?
Proszę zarkąć na obrazki okna aplikacji, w której rysowałem spiralę i nanosiłem liczby pierwsze.
Zrobiłem kilka zrzutów. Licencja CC.
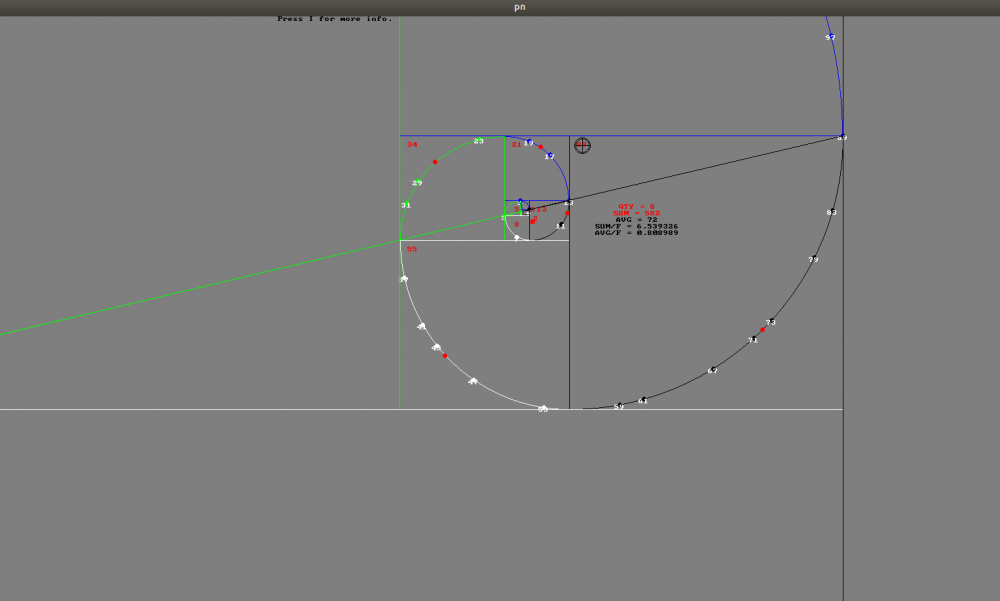
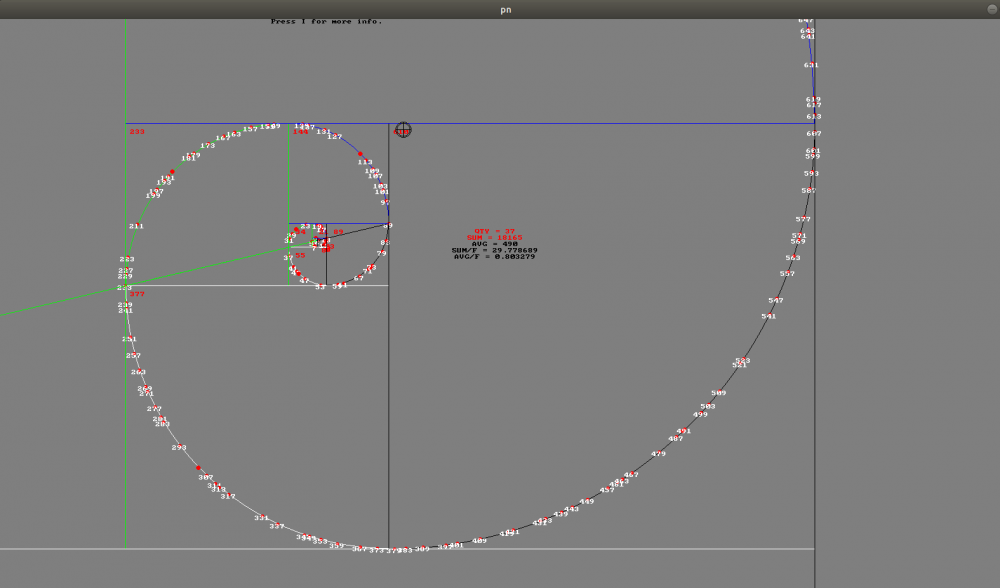
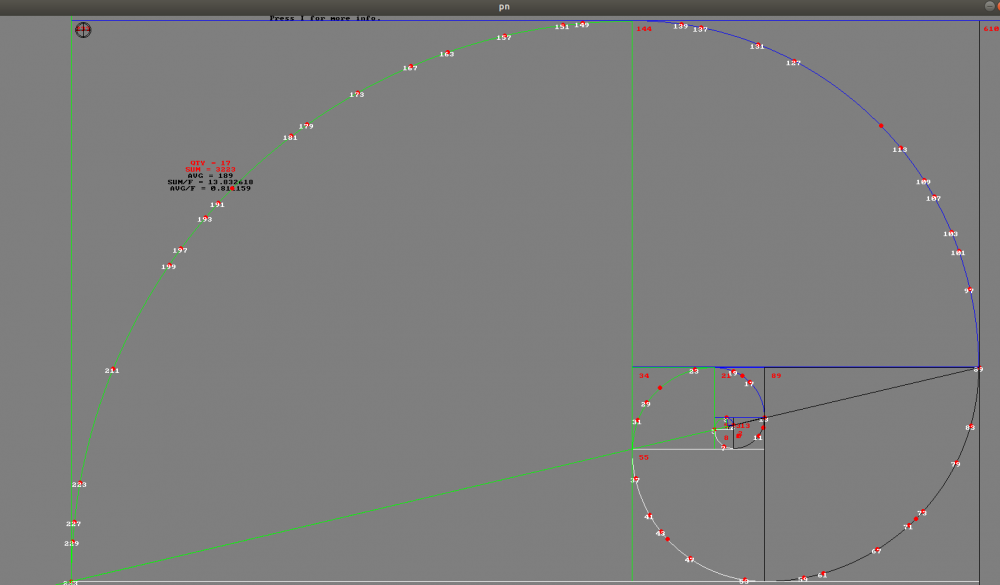
Na rysunkach na biało liczby pierwsze. Mamy dane o tych liczbach.
Wyjaśnienie:
QTY - ilość liczb pierwszych pomiędzy kolejnymi wyrazami wyrazami ciągu Fibonacciego, czyli w polu danego kwadratu.
SUM - suma liczb pierwszych pomiędzy kolejnymi wyrazami ciągu...
AVG - średnia obliczona poprzez podział sumy przez ilość, czyli SUM/QTY.
SUM/F - suma liczb pierwszych podzielona przez liczbę Fibonacciego.
AVG/F - pokazuje średnią liczb pierwszych w danym polu kwadratu, podzieloną przez liczbę Fibonacciego, to jest zawsze przybliżenie równe połowie Złotej liczby PHI/2 ≈ 0.80... z wyjątkiem trzech pierwszych liczb (2,3,5), które są równe liczbom Fibonacciego, następnie dobre przybliżenie raczej rośnie.
Gdyby ktoś był zainteresowany zabawą z aplikacją, która rysuje ta spiralę, to mogę udostępnić, proszę śmiało pisać w tej sprawie.. Jest to miniaturowy programik napisany w języku C z wykorzystaniem starej biblioteki Allegro w wersji 4.2, ale trochę wymagający pod względem mocy sprzętowej. Może działać zarówno na Windows jak i Linux.
To na razie tyle. Dzięki za dotrwanie do końca i pozdrawiam.